Handling Body Description and Mobility

from pylayers.mobility.ban.body import *
from pylayers.mobility.trajectory import Trajectory
from IPython.display import Image
from matplotlib.pyplot import *
import pylayers.util.mayautil as mau
%matplotlib inline

The body mobility is imported from motion capture files. This is the chosen manner to achieve a high degree of realism for the modeling of the human motion. Two kind of files exist :

  • c3d files are a set of point which are evolving in time

  • bvh files are a stuctured version of the motion capture.

Both type of file will be exploited in the following.

BodyCylinder data structure

To ease electromagnetic simulation a simplification of the motion capture data structure is necessary. Generally there is a large number of captured points, not all of them being useful for our modeling.

The body model is a restriction of key body segments which are transformed into \(K\) cylinders of radius \(r_k\).

The chosen body model is made of 11 cylinders. 4 cylinders decribing the two arms, 4 cylinders decribing the two legs, 2 cylinders describing the trunk and 1 cylinder for the head.

The body cylinder model is handled by the dedicated Python class call Body

To create a void body, simply instantiate a Body object from the class

John = Body()

**** Processor coding : Intel-PC

which is equivalent to :

John = Body(_filebody='John.ini',_filemocap='07_01.c3d',unit='cm')

**** Processor coding : Intel-PC

The default body filename is John.ini and the default motion capture filename is ‘07_01.c3d’. The creation of a Body consists in reading a _filebody and a _filemocap

John._show3()
mau.inotshow('John',doc=True)
../../_images/Body_7_0.png

Description of a body file

An example of a body file is given below. It is a file in ini format with 4 sections.

  • [nodes]

This section associates a node number to a c3d fils conventional node number

  • [cylinder]

This section associates a cylinder Id to a dictionnary wich contains cylinder tail head and radius information

  • [device]

This section associates a device name to a dictionnary wich contains cylinder device related information

Example of a Body file

[nodes] 0 = [STRN,T10] 1 = [CLAV,C7] 2 = [RFHD,LFHD,LBHD,RBHD] 3 = RSHO 4 = LSHO 5 = [RRAD,RHUM] 6 = [LRAD,LHUM] 7 = [RWRA,RWRB] 8 = [LWRA,LWRB] 9 = [RFWT,RBWT] 10 = [LFWT,LBWT] 11 = [RKNE,RKNI] 12 = [LKNE,LKNI] 13 = RANI 14 = LANI 15 = [RFWT, LFWT,LBWT,RBWT][cylinder] ; sternum (STRN) - clavicle (CLAV) trunku = {‘t’:0,’h’:1,’r’:0.18,’i’:0} ; bottom (BOTT) sternum (STRN) trunkb = {‘t’:15,’h’:0,’r’:0.17,’i’:10} ; clavicle (CLAV) - head (RFHD) headu = {‘t’:1,’h’:2,’r’:0.12,’i’:1} ; right elbow (RELB) right shoulder (RSHO) armr = {‘t’:5,’h’:3,’r’:0.05,’i’:2} ; left elbow (LELB) left shoulder (LSHO) arml = {‘t’:6,’h’:4,’r’:0.05,’i’:3} ; right wrist (RWRB) right elbow (RELB) forearmr = {‘t’:7,’h’:5,’r’:0.05,’i’:4} ; left wrist (LWRB) left elbow (LELB) forearml = {‘t’:8,’h’:6,’r’:0.05,’i’:5} ; right knee (RKNE) right hip (RFWT) thighr = {‘t’:11,’h’:9,’r’:0.05,’i’:6} ; left knee (LKNE) left hip (LFWT) thighl = {‘t’:12,’h’:10,’r’:0.05,’i’:7} ; right ankle (RANK) right knee (RKNE) calfr = {‘t’:13,’h’:11,’r’:0.05,’i’:8} ; left ankle (LANK) left knee (LKNE) calfl = {‘t’:14,’h’:12,’r’:0.05,’i’:9} [wearable] file = real_suit1.ini [mocap] file = serie_017_noDEC_Real.c3d ; unit of c3d file unit = mm ; number of frame to consider. if -1 : all frames nframes = -1

Bernard = Body(_filebody='Bernard.ini',_filemocap='serie_017.c3d')

**** Processor coding : Intel-PC

Loading a Motion Capture File

A .c3d motion capture file is loaded with the method ``loadC3D`` with as arguments the motion capture file and the number of frames to load.

The motion is represented as a sequence of frames stored in the ``d`` variable member.

It is possible to get the information from the C3D header by using the verbose option of the read_c3d function

# Video Frame Rate
Vrate = 120
# Inter Frame
Tframe = 1./120
# select a number of frame
nframes = 300
# Time duration of the whole selected frame sequence
Tfseq = Tframe*nframes
#
# load a .c3dmotion capture file
# this update the g.pos
#
#bc.loadC3D(filename='07_01.c3d',nframes=nframes,centered=True)

The duration of the capture is

print "Duration of the motion capture sequence", Tfseq," seconds"

Duration of the motion capture sequence 2.5  seconds

d is a MDA of shape (3,npoint,nframe). It contains all the possible configurations of the body. In general it is supposed to be a cyclic motion as an integer number of walking steps. This allows to instantiate the body configuration anywhere else in space in a given trajectory.

A specific space-time configuration of the body is called a ``topos``.

np.shape(Bernard.d)

(3, 16, 11213)

Defining a trajectory

A Trajectory is a class which :

  • derives from a pandas DataFrame

  • is a container for time,position,velocity and acceleration.

traj = Trajectory()

To define a default trajectory :

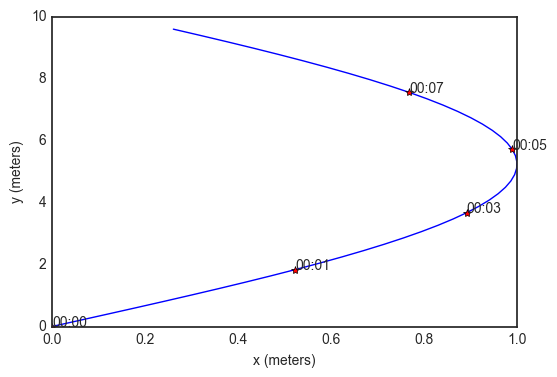
t = traj.generate()

print traj.columns

Index([u'x', u'y', u'z', u'vx', u'vy', u'vz', u'ax', u'ay', u'az', u's', u't'], dtype='object')

traj.head()
x y z vx vy vz ax ay az s t
1970-01-01 00:00:00.000000 0.000000 0.000000 -0.675584 0.299813 1.0 4.696639 -0.005505 0.0 -37.557977 0.000000 0.000000
1970-01-01 00:00:00.204082 0.061186 0.204082 0.282914 0.298689 1.0 -2.968254 -0.010989 0.0 19.938054 0.213056 0.204082
1970-01-01 00:00:00.408163 0.122143 0.408163 -0.322852 0.296446 1.0 1.100737 -0.016433 0.0 -17.065929 0.426047 0.408163
1970-01-01 00:00:00.612245 0.182642 0.612245 -0.098212 0.293093 1.0 -2.382106 -0.021814 0.0 -3.969265 0.638907 0.612245
1970-01-01 00:00:00.816327 0.242457 0.816327 -0.584356 0.288641 1.0 -3.192160 -0.027114 0.0 65.114746 0.851574 0.816327 
f,a = traj.plot()
../../_images/Body_22_0.png

settopos () method

Once the trajectory has been defined it is possible to send the body at the position corresponding to any time of the trajectory with the ``settopos`` method.

settopos takes as argument

  • A trajectory

  • A time index

traj.__repr__()

'Trajectory of agent MyNameIsNoBody with ID 1n--------------------------------------------nt (s) : 0.00 : 0.20 : 9.59ndtot (m) : 9.79nVmoy (m/s) : 1.02n                                   x         y         z        vx   vy  \n1970-01-01 00:00:00.000000  0.000000  0.000000 -0.675584  0.299813  1.0   n1970-01-01 00:00:00.204082  0.061186  0.204082  0.282914  0.298689  1.0   nn                                  vz        ax   ay         az         s  \n1970-01-01 00:00:00.000000  4.696639 -0.005505  0.0 -37.557977  0.000000   n1970-01-01 00:00:00.204082 -2.968254 -0.010989  0.0  19.938054  0.213056   nn                                   t  n1970-01-01 00:00:00.000000  0.000000  n1970-01-01 00:00:00.204082  0.204082  n'
John.settopos(traj,t=5)

plt.figure(figsize=(15,20))
for t in np.arange(traj.tmin+0.4,traj.tmax,0.5):
   John.settopos(traj,t=t)
   f,a=John.show(color='b',plane='yz',topos=True)
   axis('off')

/home/uguen/Documents/rch/devel/pylayers/pylayers/mobility/ban/body.py:2124: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
  pta =  np.array([self.topos[ax1, kta], self.topos[ax2, kta]])[:,np.newaxis]
/home/uguen/Documents/rch/devel/pylayers/pylayers/mobility/ban/body.py:2125: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
  phe =  np.array([self.topos[ax1, khe], self.topos[ax2, khe]])[:,np.newaxis]
../../_images/Body_26_1.png 
John

My name is : John

I have a Galaxy Gear device with id #1 on the left forearm witn antenna defant.vsh3
I have a cardio device with id #0 on the upper part of trunk witn antenna defant.vsh3

@ t=0.708333333333 (frameID=85),
My centroid position is [-7.87435024  5.23416696]

filewear : suit2.ini
filename : 07_01.c3d
nframes : 316
Centered : True
Mocap Speed : 13.649 m/s

Francois = Body(_filebody='Francois.ini')

**** Processor coding : Intel-PC

Francois.settopos(traj,t=6)

  • 3 : dimension of space

  • 16 : number of nodes

  • 300 : number of frames

The figure below shows the projection in a vertival plane of the body nodes.

Centering the motion

John.centered

True

In order to translate the motion in any point in space-time, a distinction is made between the real motion or topos and the centered motion capture which acts as a virtual motion.

Let \(\mathbf{p}^k\) denotes the center of gravity of the body in the (O,x,y) plane

John.center()

a = np.hstack((John.vg,John.vg[:,-1][:,np.newaxis]))

\(\mathbf{v}_g\) is the velocity vector of the gravity center of the body.

print np.shape(John.pg)
print np.shape(John.vg)

(3, 316)
(3, 316)

print John.vg[:,145]
print John.vg[:,298]

[ 0.11498696 -0.00263353  0.        ]
[ 0.10812351  0.00072441  0.        ]

At that point the body structure is centered.

The frame is centered in the xy plane by substracting from the configuration of points the projection of the body in the xy plane.

np.shape(John.d)

(3, 16, 316)

John.npoints

16

Each frame is centered above the origin. For example for a walk motion the effect of the centering is just like if the body was still walking but not moving forward exactly in the same manner as a walk on a conveyor belt.

pgc = np.sum(John.d[:,:,0],axis=1)/16
pg0 = John.pg[:,0]
print "True center of gravity", pg0
print "Center of gravity of the centered frame",pgc

True center of gravity [-17.42515686   4.93730766   0.        ]
Center of gravity of the centered frame [  4.44089210e-16  -1.05471187e-15   8.94887349e+00]

np.shape(John.pg)

(3, 316)

The current file contains 300 frames

tframe = np.arange(John.nframes)

np.shape(John.pg[0:-1,:])

(2, 316)

xg = John.pg[0,:]
yg = John.pg[1,:]
zg = John.pg[2,:]
figure(figsize=(8,8))
subplot(311)
plot(tframe,xg)
title('x component')
ylabel('m')
subplot(312)
xlabel('frame index')
title('y component')
ylabel('m')
plot(tframe,yg)
subplot(313)
xlabel('frame index')
title('Motion capture centroid trajectory')
ylabel('m')
plot(xg,yg,'.b')

d = John.pg[0:-1,1:]-John.pg[0:-1,0:-1]
smocap = np.cumsum(np.sqrt(np.sum(d*d,axis=0)))

Vmocap = smocap[-1]/Tfseq
title('Length = '+str(smocap[-1])+' V = '+str(Vmocap*3.6)+' km/h')
axis('scaled')
axis('off')
plt.tight_layout()
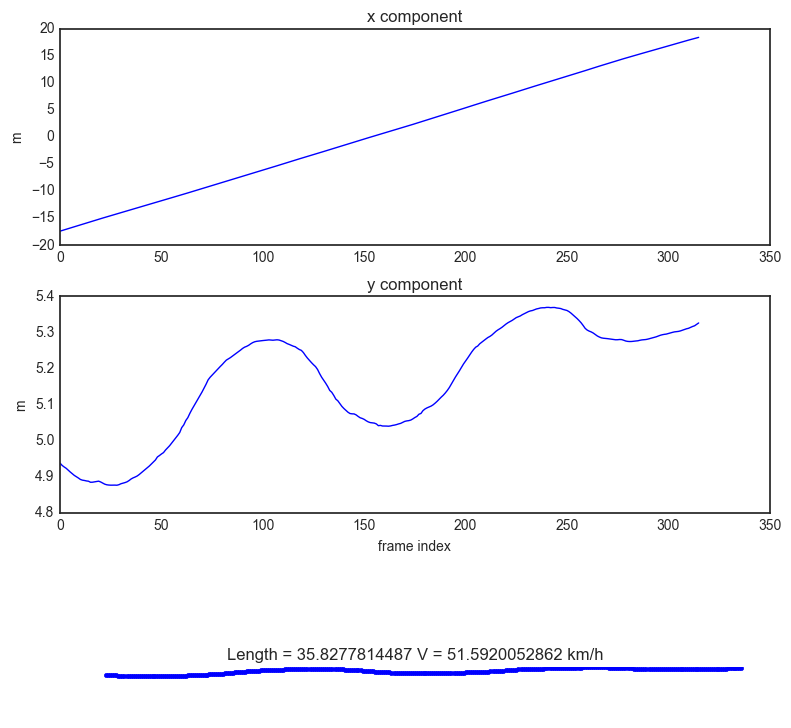
../../_images/Body_47_0.png 
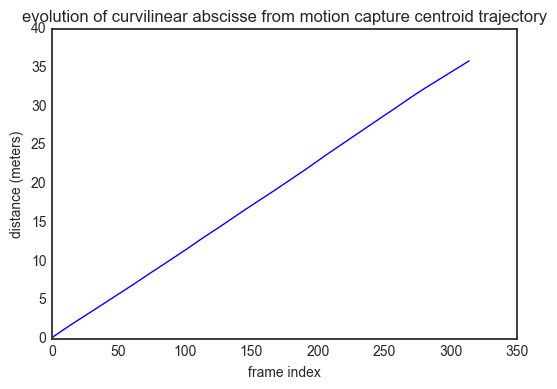
plot(smocap)
title('evolution of curvilinear abscisse from motion capture centroid trajectory')
xlabel('frame index')
ylabel('distance (meters)')

<matplotlib.text.Text at 0x7f76a3e770d0>
../../_images/Body_48_1.png

Defining a large scale trajectory

A large scale trajectory is defined in the \((O,x,y)\) plane.

traj is a data structure (Npt,2)

v = Vmocap
print v*3.6,"Kmph"

51.5920052862 Kmph

# time in seconds
time = np.arange(0,10,0.01)
x = v*time
y = np.zeros(len(time))
z = np.zeros(len(time))
traj = Trajectory()
traj.generate()
traj.tmax

9.591837

fig ,ax = traj.plot()
traj.head()
x y z vx vy vz ax ay az s t
1970-01-01 00:00:00.000000 0.000000 0.000000 -1.165661 0.299813 1.0 4.511480 -0.005505 0.0 23.463223 0.000000 0.000000
1970-01-01 00:00:00.204082 0.061186 0.204082 -0.244951 0.298689 1.0 9.299893 -0.010989 0.0 -115.745339 0.213056 0.204082
1970-01-01 00:00:00.408163 0.122143 0.408163 1.652986 0.296446 1.0 -14.321605 -0.016433 0.0 92.672156 0.426047 0.408163
1970-01-01 00:00:00.612245 0.182642 0.612245 -1.269790 0.293093 1.0 4.591080 -0.021814 0.0 -24.088894 0.638907 0.612245
1970-01-01 00:00:00.816327 0.242457 0.816327 -0.332835 0.288641 1.0 -0.325021 -0.027114 0.0 30.057229 0.851574 0.816327
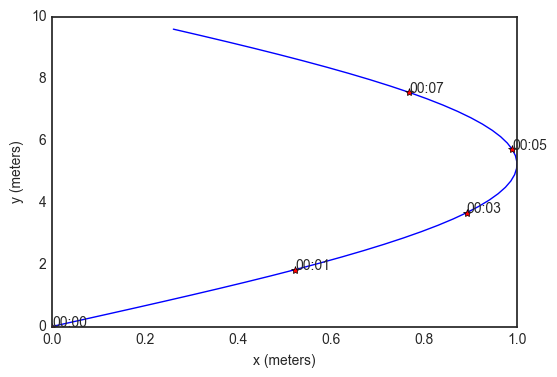
../../_images/Body_52_1.png

Trajectory

posvel()

The posvel() method (position and velocity) takes as arguments the following parameters

  • traj a plane trajectory object.

  • \(t_k\) time for evaluation of topos

  • \(T_{fs}\) duration of the periodic motion frame sequence

and returns

  • the frame index \(k_f = \lfloor \frac{t_k \pmod{T_{fs}}}{t_f} \rfloor\)

  • the trajectory index \(k_t = \lfloor t_k \rfloor\)

  • velocity unitary vector along motion capture frame \(\hat{\mathbf{v}}_s = \frac{\mathbf{p}^g[k_f]-\mathbf{p}^g[k_f-1]}{|\mathbf{p}^g[k_f]-\mathbf{p}^g[k_f-1]|}\)

  • $:raw-latex:hat{mathbf{w}}_s = :raw-latex:`\mathbf{\hat{z}}` :raw-latex:`\times `:raw-latex:`hat{mathbf{v}}`_s $

  • velocity unitary vector along trajectory \(\hat{\mathbf{v}}_t = \frac{\mathbf{p}^t[k_t]-\mathbf{p}^g[k_t-1]}{|\mathbf{p}^g[k_t]-\mathbf{p}^t[k_t-1]|}\)

  • $:raw-latex:hat{mathbf{w}}_t = :raw-latex:`\mathbf{\hat{z}}` :raw-latex:`\times `:raw-latex:`hat{mathbf{v}}`_t $

\(t_f = \frac{T_{fs}}{Nf}\) is the interframe time or frame sampling period, it is equal to the whole duration of the motion sequence \(T_{fs}\) divided by the number of frames

settopos is a method which takes as argument :

  • traj a plane trajectory (Npt,2)

  • \(t_k\) time for evaluation of topos

In further version of the class, this function will be modified to avoid passing the whole trajectory.

John.settopos(traj=traj,t=3)

There is now a new data structure in the Body objet. This data structure is called a topos.

print np.shape(John.topos)

(3, 16)

John.topos

array([[  0.74198686,   0.76931593,   1.80846633,   2.26719915,
         -0.91675363,   3.25586636,  -1.86053098,   3.82194596,
         -2.06245933,   2.15021298,  -0.55180885,   2.02586803,
         -0.94510502,   1.36586716,  -0.57366714,   0.79920206],
       [  3.75720113,   3.13644711,   2.8414143 ,   2.20063108,
          2.6901425 ,   1.78826275,   3.20212316,   1.7696506 ,
          4.042258  ,   3.29688912,   3.60268634,   2.76571804,
          3.90430304,   2.24259271,   1.0241781 ,   3.44978773],
       [ 12.24457275,  13.88075684,  16.00988037,  14.0978418 ,
         14.3736377 ,  10.74208496,  11.07206543,   7.98268372,
          8.47460388,   9.31935974,   9.1988916 ,   4.30262299,
          4.54000305,   0.44698982,   1.7794635 ,   9.25912567]])

John.settopos(traj=traj,t=1)
fig,ax=John.plot3d(topos=True,col='#87CEEB')
John.settopos(traj=traj,t=2)
John.plot3d(topos=True,fig=fig,ax=ax,col='#7EC0EE')
John.settopos(traj=traj,t=3)
John.plot3d(topos=True,fig=fig,ax=ax,col='#6A5ACD')
John.settopos(traj=traj,t=4)
John.plot3d(topos=True,fig=fig,ax=ax,col='#7A67EE')
John.settopos(traj=traj,t=5)
John.plot3d(topos=True,fig=fig,ax=ax,col='#473C8B')

/home/uguen/Documents/rch/devel/pylayers/pylayers/mobility/ban/body.py:1768: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
  pA = self.topos[:, e0].reshape(3,1)
/home/uguen/Documents/rch/devel/pylayers/pylayers/mobility/ban/body.py:1769: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
  pB = self.topos[:, e1].reshape(3,1)

(<matplotlib.figure.Figure at 0x7f76aef51390>,
 <matplotlib.axes._subplots.Axes3DSubplot at 0x7f76a38399d0>)
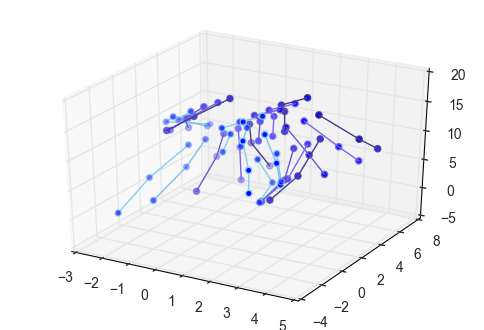
../../_images/Body_58_2.png

Definition of Several Coordinates systems

Each cylinder of the Body model bears one specific coordinate system.

One or several cylinder coordinate systems can be chosen to define the Body Local Coordinates System (BLCS) which is required for motion capture (BLCS) applications.

In general, the origin will be chosen on a position which is the most time invariant as on the chest or the back.

Those frames of references are all defined in the Global Coordinate System (GCS) of the scene.

Construction of the Cylinder Coordinate System (CCS)

The method setccs() is used to associate a Cylinder Coordinate System (CCS) to each cylinder of the bodyCylinder model. Notice that those cylinders coordinates systems are not known by the localization application. The localization application will define the BLCS from the position of radiating devices placed on the body surface.

Each basis is constructed with the function from geomutil.onbfromaxe() : orthonormal bases from axes. This function takes 2 sets of \(n\) points \(\mathbf{p}_{A,n}\) and \(\mathbf{p}_{B,n}\) as input and provides an orthonormal basis as output.

3 unitary vectors are constructed :

\[\hat{\mathbf{w}}_n = \frac{\mathbf{p}_B-\mathbf{p}_A}{| \mathbf{p}_B-\mathbf{p}_A |}\]
\[\hat{\mathbf{u}}_n = \frac{\hat{\mathbf{v}}_g - (\hat{\mathbf{v}}_g.{\hat{\mathbf{w}}_n}) \mathbf{\hat{w}}_n}{|\hat{\mathbf{v}_g} - (\hat{\mathbf{v}_g}.{\hat{\mathbf{w}}_n}) \mathbf{\hat{w}}_n|}\]
\[\hat{\mathbf{v}}_n = \mathbf{\hat{w}}_n \times \mathbf{\hat{u}}_n\]

Where \(\hat{\mathbf{v}}_g\) is the unit velocity vector along actual trajectory.

The outpout of geomutil.onbframe is an MDA \((3\times n \times 3)\) of \(n\) unitary matrices aggregated along axis 1

\[\mathbf{T}_n=[\hat{\mathbf{u}}_n, \hat{\mathbf{v}}_n, \hat{\mathbf{w}}_n]\]

To create the CCS :

John.setccs()

import scipy.linalg as la
print "ccs dimensions : ",np.shape(John.ccs)
print John.ccs[0,:,:]
print "Check determinant : ", la.det(John.ccs[0,:,:])

ccs dimensions :  (11, 3, 3)
[[ 0.94678656  0.05306765 -0.31745715]
 [-0.06834689  0.99696857 -0.03718026]
 [ 0.31452173  0.05689898  0.94754345]]
Check determinant :  1.0

Create a Wireframe body representation from the body graph model

Placing a dcs (Device Coordinate System ) on the cylinder

A DCS is refered by 4 numbers \((Id,l,h,\alpha)\)

  • Id : Cylinder Id

  • l : length along cylinder

  • h : height above cylinder generatrix

  • alpha : angle from front direction (degrees)

Id = 4 # 4 Left Arm
l  = 0.1 # Longitudinal coordinates
h  = 0.03 # height
alpha = 45 # angle degrees

John.dcyl
{'arml': 3,
 'armr': 2,
 'calfl': 9,
 'calfr': 8,
 'forearml': 5,
 'forearmr': 4,
 'headu': 1,
 'thighl': 7,
 'thighr': 6,
 'trunkb': 10,
 'trunku': 0}

{'arml': 3,
 'armr': 2,
 'calfl': 9,
 'calfr': 8,
 'forearml': 5,
 'forearmr': 4,
 'headu': 1,
 'thighl': 7,
 'thighr': 6,
 'trunkb': 10,
 'trunku': 0}

Rotate Matrix around z

John.settopos(traj=traj,t=6,cs=True)

John.dcyl
{'arml': 3,
 'armr': 2,
 'calfl': 9,
 'calfr': 8,
 'forearml': 5,
 'forearmr': 4,
 'headu': 1,
 'thighl': 7,
 'thighr': 6,
 'trunkb': 10,
 'trunku': 0}

{'arml': 3,
 'armr': 2,
 'calfl': 9,
 'calfr': 8,
 'forearml': 5,
 'forearmr': 4,
 'headu': 1,
 'thighl': 7,
 'thighr': 6,
 'trunkb': 10,
 'trunku': 0}

John.show3(topos=True,dcs=True)

/home/uguen/Documents/rch/devel/pylayers/pylayers/antprop/antenna.py:1715: RuntimeWarning: divide by zero encountered in log10
  self.GdB = 10*np.log10(self.G)
/home/uguen/Documents/rch/devel/pylayers/pylayers/mobility/ban/body.py:2294: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
  pA = self.topos[:,e0].reshape(3,1)
/home/uguen/Documents/rch/devel/pylayers/pylayers/mobility/ban/body.py:2295: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
  pB = self.topos[:,e1].reshape(3,1)

John.show3(topos=True,pattern=True)