The transmission channel

%matplotlib inline

from pylayers.antprop.rays import *
import scipy.fftpack as fft
from pylayers.gis.layout import *
from pylayers.antprop.signature import *
from pylayers.simul.link import *
from pylayers.antprop.channel import *
import pylayers.signal.waveform as wvf
from pylayers.simul.simulem import *
import matplotlib.pyplot as plt
import time

We start by constructing a propagation channel with the dedicated class DLink. We specify a Layout as well as the two extremities of the link. Antennas are also specified. The frequency range is determined by the frequency range of antennas.

L = Layout('defstr.ini')
L.Gs.node[1]['ss_name']=['WOOD','AIR','METAL']
L.build()
tx=array([759,1114,1.0])
rx=array([761,1114,1.5])
fGHz = np.linspace(2,6,401)
Aa = Antenna('Omni',fGHz=fGHz)
Ab = Antenna('Omni',fGHz=fGHz)
Lk = DLink(L=L,a=tx,b=rx,Aa=Aa,Ab=Ab)

building Layout ...
check len(ncycles) == 2 passed

The full evaluation and hdf5 storage of the channel is done with the eval function. The force option is for forcing a full reevaluation.

ak,tauk=Lk.eval(force=True)

f = plt.figure(figsize=(15,15))
f,a=Lk.C.show(cmap='jet',typ='l20',fig=f,vmin=-100,vmax=-20,fontsize=22)
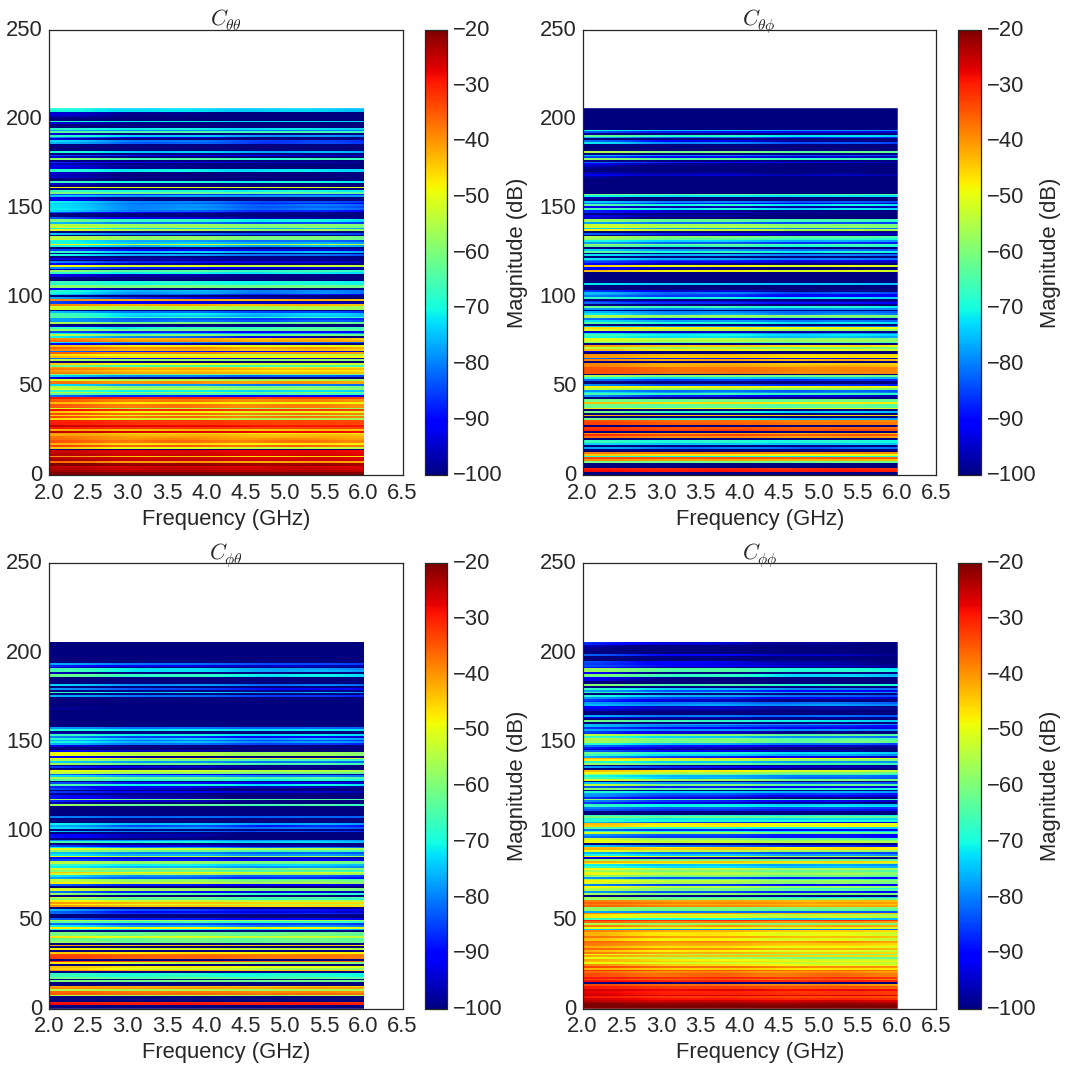
../../_images/Channel_7_0.png

The transmission channel is stored in H

Lk.H

Tchannel : Ray transfer function (Nray x Nr x Nt x Nf)
-----------------------------------------------------
freq : 2.0 6.0 401
shape  : (206, 1, 1, 401)
tau (min, max) : 6.87184270936 76.4671316464
dist (min,max) : 2.06155281281 22.9401394939
Friis factor -j c/(4 pi f) has been applied
 calibrated : No
 windowed : No

Once the channel has been calculated, we define an Impulse Radio Waveform.

fGHz=np.arange(2,12,.1)
wav = wvf.Waveform(fcGHz=5,bandGHz=3)

wav.show()
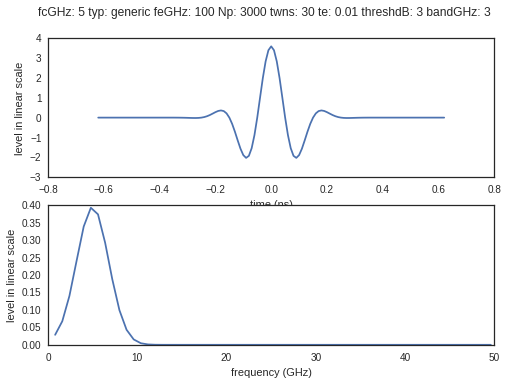
../../_images/Channel_12_0.png

is an object which contains all the information about the propagation channel.

f,a=Lk.show()
../../_images/Channel_14_0.png

The Ctilde channel can be sorted with respect to delay

Lk.H

Tchannel : Ray transfer function (Nray x Nr x Nt x Nf)
-----------------------------------------------------
freq : 2.0 6.0 401
shape  : (206, 1, 1, 401)
tau (min, max) : 6.87184270936 76.4671316464
dist (min,max) : 2.06155281281 22.9401394939
Friis factor -j c/(4 pi f) has been applied
 calibrated : No
 windowed : No

len(Lk.fGHz)

402

f = plt.figure(figsize=(20,10))
f,a =Lk.H.show(fig=f,cmap='jet')
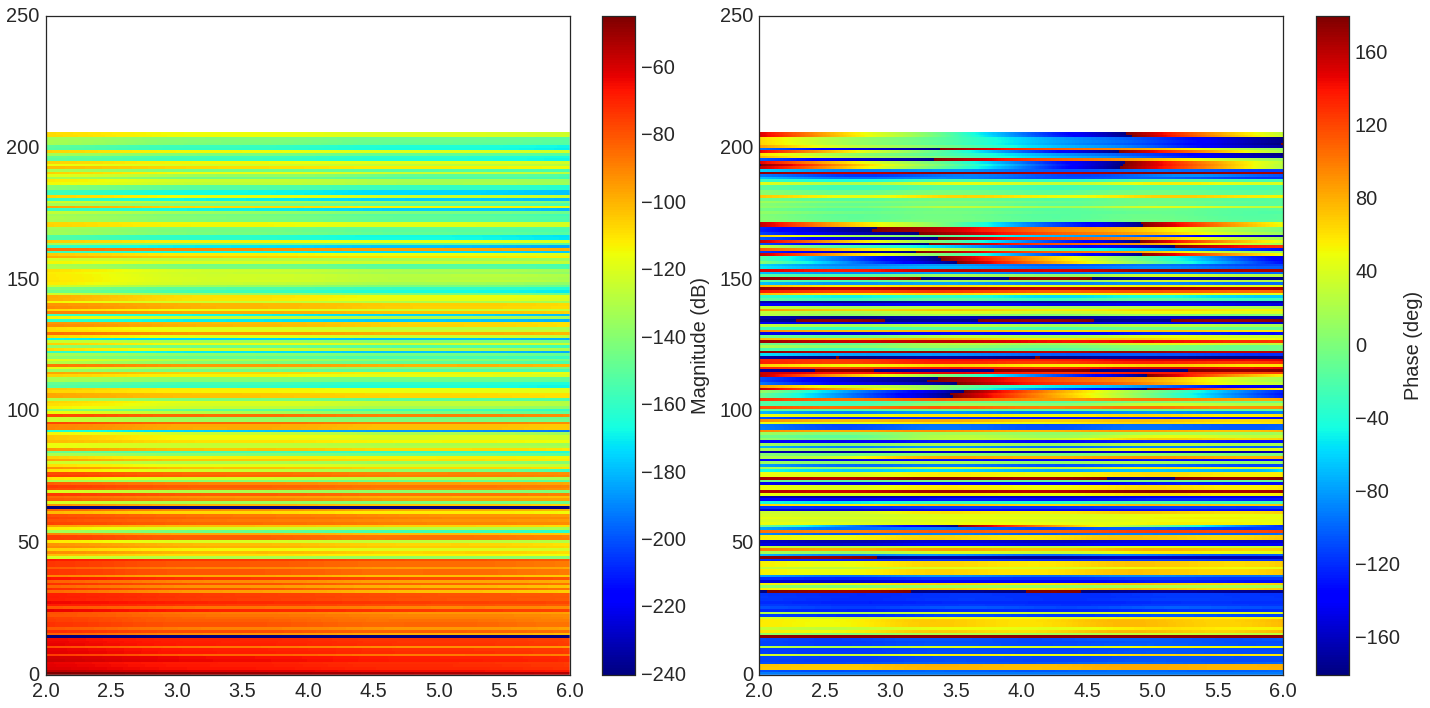
../../_images/Channel_18_0.png

The Friis factor

The Friis factor is :

\[\alpha=\frac{-jc}{4\pi f}\]

This factor is fundamental and has to be applied only once. By default the link is evaluated with the Friis factor : isFriis=True. This can be checked at the end of the repr of H.

Lk.H

Tchannel : Ray transfer function (Nray x Nr x Nt x Nf)
-----------------------------------------------------
freq : 2.0 6.0 401
shape  : (206, 1, 1, 401)
tau (min, max) : 6.87184270936 76.4671316464
dist (min,max) : 2.06155281281 22.9401394939
Friis factor -j c/(4 pi f) has been applied
 calibrated : No
 windowed : No

Emean=Lk.H.energy(mode='mean')
Eint=Lk.H.energy(mode='integ')
Ecenter=Lk.H.energy(mode='center')
Efirst=Lk.H.energy(mode='first')
Elast=Lk.H.energy(mode='last')

print Efirst[0],Elast[0]

[[  3.35253916e-05]] [[  3.72504352e-06]]

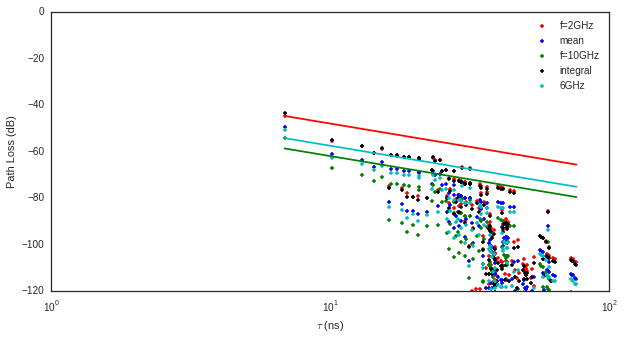
On the figure below we have selected a LOS situation and we compare the energy for each path with the LOS values (the straight line). The 3 straight lines coresponds to the Free space path loss formula for 3 frequencies (f = 2GHz,f=6GHz,f=10GHz). For those 3 frequencies the first path is perfectly on the curve, which is a validation the observed level.

Lk.H.y.shape

(206, 1, 1, 401)

f1 = 2
f2 = 10
f3 = 6
fig = plt.figure(figsize=(10,5))
a = plt.semilogx(Lk.H.taud,10*np.log10(Efirst[:,0,0]),'.r',label='f=2GHz')
a = plt.semilogx(Lk.H.taud,10*np.log10(Emean[:,0,0]),'.b',label='mean')
a = plt.semilogx(Lk.H.taud,10*np.log10(Elast[:,0,0]),'.g',label='f=10GHz')
a = plt.semilogx(Lk.H.taud,10*np.log10(Eint[:,0,0]),'.k',label='integral')
a = plt.semilogx(Lk.H.taud,10*np.log10(Ecenter[:,0,0]),'.c',label='6GHz')
plt.xlabel(r'$\tau$ (ns)')
plt.ylabel('Path Loss (dB)')
LOS1 = -32.4-20*np.log10(Lk.H.taud*0.3)-20*np.log10(f1)
LOS2 = -32.4-20*np.log10(Lk.H.taud*0.3)-20*np.log10(f2)
LOS3 = -32.4-20*np.log10(Lk.H.taud*0.3)-20*np.log10(f3)
plt.semilogx(Lk.H.taud,LOS1,'r')
plt.semilogx(Lk.H.taud,LOS2,'g')
plt.semilogx(Lk.H.taud,LOS3,'c')
plt.semilogx(tauk,20*np.log10(np.sum(np.sum(ak,axis=2),axis=1)),'+')
plt.ylim([-120,0])
plt.legend()

<matplotlib.legend.Legend at 0x7f5539cb78d0>
../../_images/Channel_25_1.png 
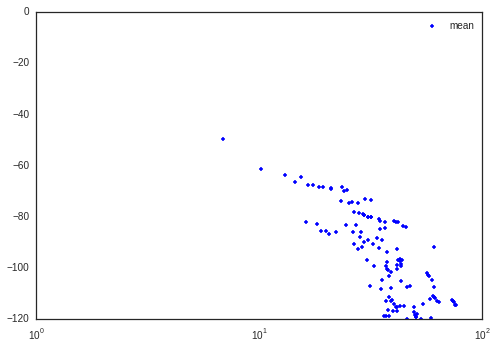
a = plt.semilogx(Lk.H.taud,10*np.log10(Emean[:,0,0]),'.b',label='mean')
plt.semilogx(tauk,20*np.log10(np.sum(np.sum(ak,axis=2),axis=1)),'+')
plt.ylim([-120,0])
plt.legend()

<matplotlib.legend.Legend at 0x7f553b979090>
../../_images/Channel_26_1.png 
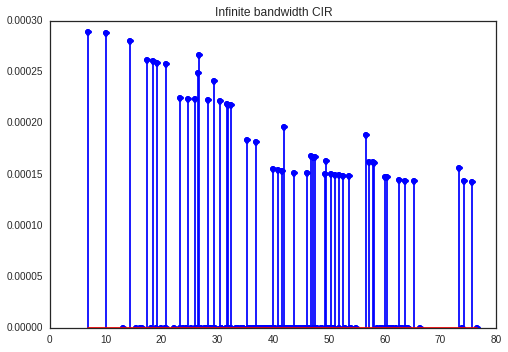
CIR=TUchannel(tauk,np.zeros(len(tauk)))
CIR.aggcir(ak,tauk)
CIR.stem()
plt.title('Infinite bandwidth CIR')

<matplotlib.text.Text at 0x7f553bb7c650>
../../_images/Channel_27_1.png 
MeanDelay = CIR.tau_moy()
DelaySpread = CIR.tau_rms()
print MeanDelay,DelaySpread

36.619045782 13.4093554011

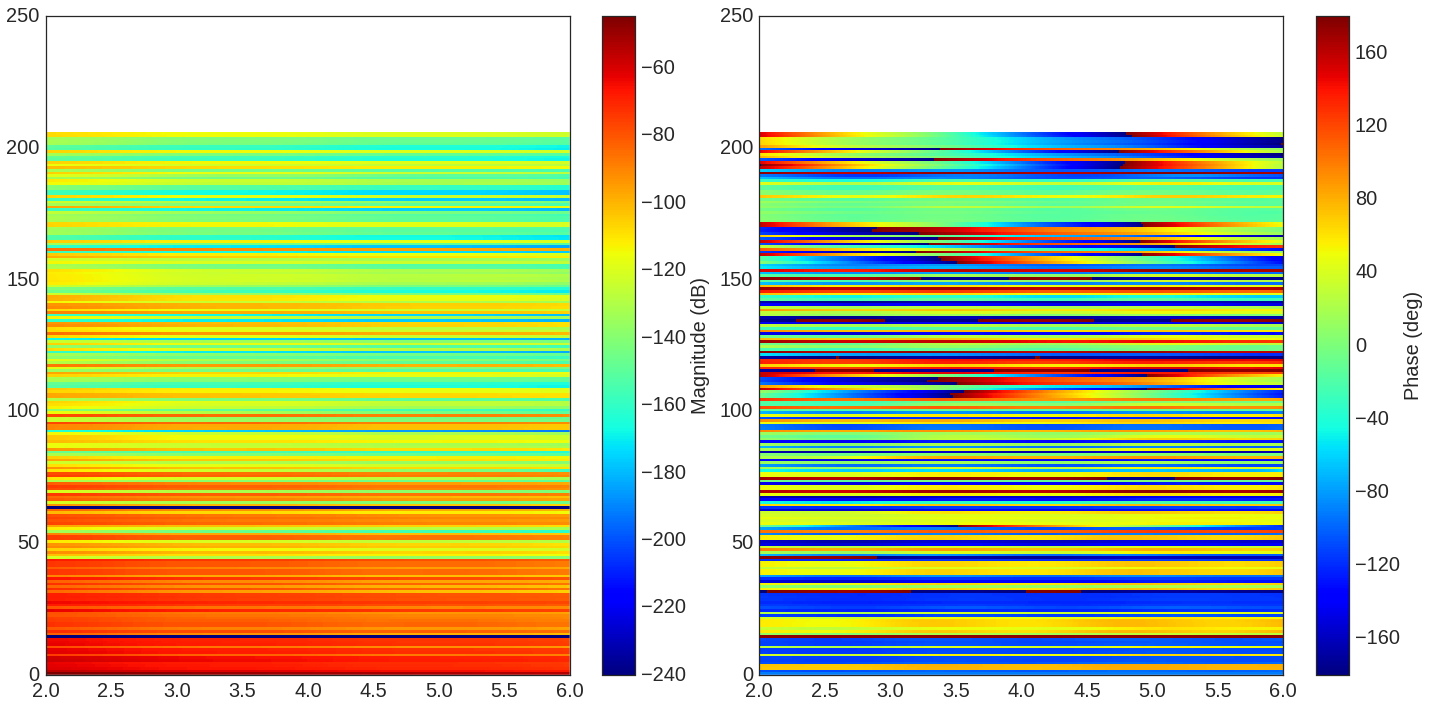
f = plt.figure(figsize=(20,10))
f=Lk.H.show(cmap='jet',fig=f)
../../_images/Channel_29_0.png

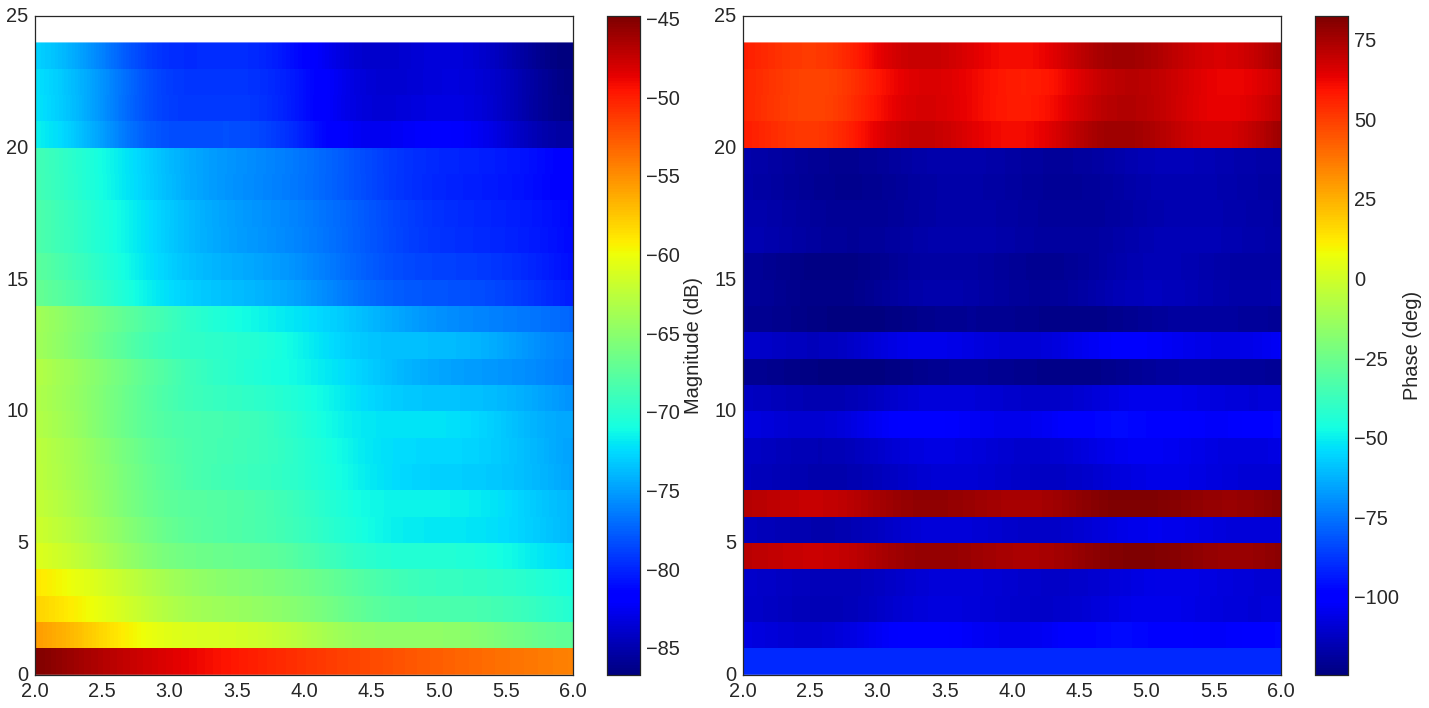
The cut method applies an energy thresholding on the transmission channel.

Lk.H.cut()

f = plt.figure(figsize=(20,10))
f=Lk.H.show(cmap='jet',fig=f)
../../_images/Channel_32_0.png

The tap method

The tap methods takes as parameters : + The system bandwidth \(W\) expressed in MHz + The two extremities velocities \(V_a\) and \(V_b\) + The number of taps to be evaluted \(N_{tap}\) + The number of time samples \(N_m\) + The number of spatial realizations \(N_s\)

This method returns a Multi Dimensional Array \(htap(f,s,m,tap)\)

htap has 4 axes.

  • axis 0 is frequency,

  • axis 1 is spatial realization

  • axis 2 is discrete time

  • axis 3 is tap index

Va = 10
Vb = 10
fcGHz = 4.5
Nm = 50
Ns = 10
WMHz = 20
Ntap = 10

# htap,b,c,d = Lk.H.tap(WMHz=WMHz,Ns=Ns,Nm=Nm,Va=Va,Vb=Vb,Ntap=Ntap)

#np.shape(htap)

The second parameter is the time integration of htap

  • axis 0 i frequency

  • axis 2 is spatial (realization)

  • axis 2 is tap

# b.shape

# np.shape(c)

# d.shape

The figure below illustrates the joint frequency and spatial fluctuation for the first channel tap. :exit

#img = plt.imshow(abs(b[:,:,0]),interpolation='nearest',extent=(0,1000,fGHz[-1],fGHz[0]))
#plt.axis('tight')
#plt.colorbar()
#plt.xlabel('spatial realizations')
#plt.ylabel('Frequency GHz')

#f = plt.figure(figsize=(10,4))
#h = plt.hist(np.real(b[0,:,0])*1e5,40,normed=True)

#mmax = 0.3*WMHz*1e6/(2*fcGHz*(Va+Vb))
#tmaxms = 1000*mmax/(WMHz*1e6)
#plt.imshow(abs(c[:,:,1]),interpolation='nearest',extent=(0,tmaxms,fGHz[-1],fGHz[0]))
#plt.axis('tight')
#plt.colorbar()
#plt.xlabel('Discrete Time (ms)')
#plt.ylabel('frequency (GHz)')

#plt.plot(abs(c[0,:,0]))

#h = c[:,:,2]

#from pylayers.util.mayautil import *
#m=VolumeSlicer(data=abs(htap[:,0,:,:]))
#m.configure_traits()